As a baseline we'd recommend raising three times the big blind with hand like like 22+/AT+/KJ+/89s-JQs/A2s-A5s. This is 15.5% of hands. If we have tight players on our left we can start to raise. Which poker stats are most important? Our poker HUD software offers a large amount of statistics. Adding up the values for each of these possibilities gives us a value for the hand of $1.32 and tells us that discarding the low pair is our best option. Your approach to playing video poker hands should now be obvious. You should always play the hand with the highest rank or value.
The ongoing $200/$400 heads-up no-limit hold'em match between Doug Polk and Daniel Negreanu has captured the attention of the poker world, particularly with the dearth of other action of interest out there.
Two legends of poker battling back and forth for pots worth sometimes hundreds of thousands of dollars has naturally produced some interesting hands that merit a closer look from a strategic point of view.
Getting an expert's perspective on such a hand isn't easy considering how few HUNL specialists are out there and qualified to comment critically on these stakes, but PokerNews did manage to get hold of one: Kevin Rabichow. The high-stakes pro and Run It Once Poker ambassador graciously agreed to help break down a pot I found fascinating while covering the action.
The hand can be viewed here but for those not wishing to relive it in video form, here's how the action goes:
Negreanu raised to $960 on the button and Polk reraised to $3,945. Negreanu four-bet to $10,800 and Polk called, bringing a flop. Both players checked and the turn was the . Polk led out $6,479 and Negreanu called. On the river, Polk shoved for $32,132. Negreanu quickly called with and won the showdown against to scoop a $98K pot.
PokerNews: How does being 125 bigs deep change preflop strategy with these hands if at all? Is everything they do here standard?
Kevin Rabichow: The interesting decision preflop as you get deeper is how do you adjust what you're going to stack off compared to three-bet-call or just call. Maybe you three-bet less than usual here but I still think this hand's always a three-bet. Sometimes you can five-bet all in for 100 bigs but maybe not 125.
On the flop, we see both players check. I assume that's also pretty standard or is there an argument to bet because this is a good flop for the four-bettor's range, and aces and queens are potentially bad turns than can cost you a pretty big pot?
It's common for button to bet range on this flop. The key thing is it's king-high. When the board comes king-high, the really important thing in heads-up preflop ranges is that button will have all ace-kings and big blind never has any ace-kings. You can't say that as confidently in other formats but in heads up you can.
Daniel should probably just bet. If Doug folds queen-jack or something with an ace in it, you get some equity out of the pot and can charge a gutshot or open-ended straight draw. I think it's a little non-standard not to bet. If I was gonna check anything, my first choice would be queens or jacks, though. If you're gonna play checks, this hand is up there.
After a turn, Doug leads one-third of pot. Is this for standard for value and protection?
Doug is very GTO-focused. He's trying to just play well and learn from the solver. The solver wouldn't check very much. is the type of hand that wants to lead small. It does depend on what types of hands Daniel is checking back though.
We had seen Daniel occasionally check as strong as top pair in these four-bet pots.
That makes it really tough if he's checking . What Doug has to ask himself is, 'Is this hand good enough to bet for protection?' Not just does it want to because it clearly does.
Keep in mind stuff like queen-six suited or ace-five suited are preflop bluffs and made a weak pair. That's part of the range that gets overlooked heads up. Daniel's gonna bluff with raggedy , . He could have pair of sixes or fives. If he folds out something like that has six clean outs, that's also great for him.
It's kind of thin. I think it's still clear the bet is fine.
We see a pot-sized shove on the river. I assume it's for value? Is this too thin?
I think on the surface, it's a pretty normal shove in heads up. In this situation, it's a little thin. The key thing here is Doug's out of position. It's a thin value shove for one pot-sized bet, so that makes the math pretty easy. If he was to check and get shoved on he needs 33% to check-call. Traditionally if you make a value-bet, you want to get called by a range you're ahead of. When he shoves and gets called, maybe he's got 43% equity.
It gets weird out of position with these thin, in-between hands. But, he's ahead of , , even which might hero. A rivered pair of sevens which is unlikely but maybe a hand that bluffed preflop could have gotten here. There's stuff that he beats but it's certainly not thrilling.
But, Doug is someone who bluffs a lot, and Daniel will make hero calls. Maybe Doug doesn't think check performs very well. Maybe he's saying if he has or it's a cooler, which I kind of agree with. I think Doug's shoving for value fully expecting to lose more than time.
So, even though he might be beat more than half of the time he's called, jam can still be good for value?
You have to look at the [expected value] of check as a whole versus the EV of jam as a whole. If he jams, he always gets called by better hands and sometimes by worse hands. When he checks, Daniel will always check back the hands Doug beats. But, the concern is he will bluff sometimes and he will value-bet all the better hands. If he feels he cannot check-fold, then value-betting becomes worth considering.
Does block-betting the river make any sense?
From what I've seen of Daniel's game, I think block is very likely the best play. That would probably be my first choice. I think it's a good play. It's quite possible Doug randomized for his sizing or just kind of got caught up in making a greedy sizing choice.
Blocking river in a spot like this is definitely part of good strategy. The likely response we're hoping for is Daniel calls with . If that's the play he takes even a little bit of time, that's an amazing result. We get extra value from fives and sixes and don't lose the max against and .
What do regular players need to understand about heads-up no-limit that makes this shove good?
I think the framework within heads-up no-limit is to realize like and , even if we think Daniel is conservative, it's not an overwhelming majority of his range. We can't focus so quickly on that part of his range. Because preflop ranges are so wide, it's important to remember that ace-high needs to call the turn and and need to call river a lot of the time against a jam. Just recognizing that the overall strategy good heads-up no-limit players use in this spot isn't overly focused on the top of Daniel's range. There's all this trash and all these other weak hands.
What parts of heads-up no-limit can fans watching take and try to apply to their own games?
Honestly, it's probably just aggression. Recognizing the value of finding bets and stacking off uncomfortably light. It trickles to the rest of your strategy. The benefit of Doug having plays like this that are thin and look wild is you allow yourself to be aggressive with the bluffs in your range and find thinner value bets as a result. Your aggression goes up and you win more pots.
Almost all players are not aggressive enough, even professional players. Six-max, tournaments...players are by and large not aggressive enough. Here's a player at the top of the game on the biggest stage and he's going after it every pot. That's something worth trying to emulate, I think.
Kevin Rabichow is a high-stakes professional and coach for Run It Once Training. You can check out his personal coaching page here and reach him on Twitter with any questions or comments.
Tags
Doug PolkDaniel NegreanuCash PokerOnline PokerRelated Players
Daniel NegreanuDoug Polk
This post works with 5-card Poker hands drawn from a standard deck of 52 cards. The discussion is mostly mathematical, using the Poker hands to illustrate counting techniques and calculation of probabilities
Working with poker hands is an excellent way to illustrate the counting techniques covered previously in this blog – multiplication principle, permutation and combination (also covered here). There are 2,598,960 many possible 5-card Poker hands. Thus the probability of obtaining any one specific hand is 1 in 2,598,960 (roughly 1 in 2.6 million). The probability of obtaining a given type of hands (e.g. three of a kind) is the number of possible hands for that type over 2,598,960. Thus this is primarily a counting exercise.
___________________________________________________________________________
Preliminary Calculation
Usually the order in which the cards are dealt is not important (except in the case of stud poker). Thus the following three examples point to the same poker hand. The only difference is the order in which the cards are dealt.
These are the same hand. Order is not important.
The number of possible 5-card poker hands would then be the same as the number of 5-element subsets of 52 objects. The following is the total number of 5-card poker hands drawn from a standard deck of 52 cards.
The notation is called the binomial coefficient and is pronounced 'n choose r', which is identical to the number of -element subsets of a set with objects. Other notations for are , and . Many calculators have a function for . Of course the calculation can also be done by definition by first calculating factorials.
Poker Value Chart
Thus the probability of obtaining a specific hand (say, 2, 6, 10, K, A, all diamond) would be 1 in 2,598,960. If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of all diamond cards? It is
This is definitely a very rare event (less than 0.05% chance of happening). The numerator 1,287 is the number of hands consisting of all diamond cards, which is obtained by the following calculation.
The reasoning for the above calculation is that to draw a 5-card hand consisting of all diamond, we are drawing 5 cards from the 13 diamond cards and drawing zero cards from the other 39 cards. Since (there is only one way to draw nothing), is the number of hands with all diamonds.
If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of cards in one suit? The probability of getting all 5 cards in another suit (say heart) would also be 1287/2598960. So we have the following derivation.
Thus getting a hand with all cards in one suit is 4 times more likely than getting one with all diamond, but is still a rare event (with about a 0.2% chance of happening). Some of the higher ranked poker hands are in one suit but with additional strict requirements. They will be further discussed below.
Another example. What is the probability of obtaining a hand that has 3 diamonds and 2 hearts? The answer is 22308/2598960 = 0.008583433. The number of '3 diamond, 2 heart' hands is calculated as follows:
One theme that emerges is that the multiplication principle is behind the numerator of a poker hand probability. For example, we can think of the process to get a 5-card hand with 3 diamonds and 2 hearts in three steps. The first is to draw 3 cards from the 13 diamond cards, the second is to draw 2 cards from the 13 heart cards, and the third is to draw zero from the remaining 26 cards. The third step can be omitted since the number of ways of choosing zero is 1. In any case, the number of possible ways to carry out that 2-step (or 3-step) process is to multiply all the possibilities together.
___________________________________________________________________________
The Poker Hands
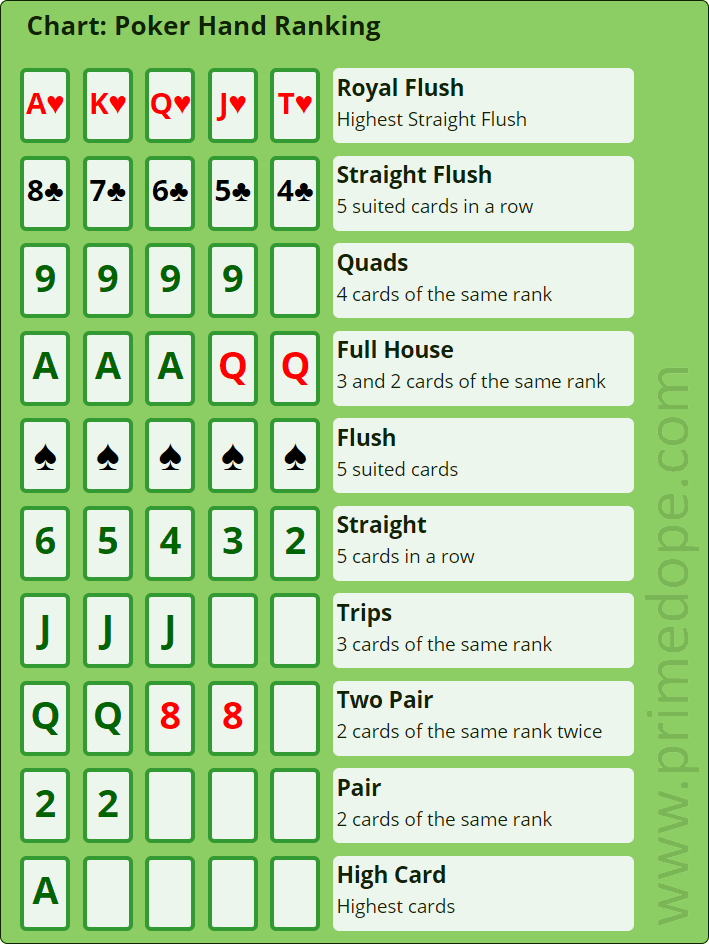
Here's a ranking chart of the Poker hands.
The chart lists the rankings with an example for each ranking. The examples are a good reminder of the definitions. The highest ranking of them all is the royal flush, which consists of 5 consecutive cards in one suit with the highest card being Ace. There is only one such hand in each suit. Thus the chance for getting a royal flush is 4 in 2,598,960.
Royal flush is a specific example of a straight flush, which consists of 5 consecutive cards in one suit. There are 10 such hands in one suit. So there are 40 hands for straight flush in total. A flush is a hand with 5 cards in the same suit but not in consecutive order (or not in sequence). Thus the requirement for flush is considerably more relaxed than a straight flush. A straight is like a straight flush in that the 5 cards are in sequence but the 5 cards in a straight are not of the same suit. For a more in depth discussion on Poker hands, see the Wikipedia entry on Poker hands.
The counting for some of these hands is done in the next section. The definition of the hands can be inferred from the above chart. For the sake of completeness, the following table lists out the definition.
Definitions of Poker Hands
| Poker Hand | Definition | |
|---|---|---|
| 1 | Royal Flush | A, K, Q, J, 10, all in the same suit |
| 2 | Straight Flush | Five consecutive cards, |
| all in the same suit | ||
| 3 | Four of a Kind | Four cards of the same rank, |
| one card of another rank | ||
| 4 | Full House | Three of a kind with a pair |
| 5 | Flush | Five cards of the same suit, |
| not in consecutive order | ||
| 6 | Straight | Five consecutive cards, |
| not of the same suit | ||
| 7 | Three of a Kind | Three cards of the same rank, |
| 2 cards of two other ranks | ||
| 8 | Two Pair | Two cards of the same rank, |
| two cards of another rank, | ||
| one card of a third rank | ||
| 9 | One Pair | Three cards of the same rank, |
| 3 cards of three other ranks | ||
| 10 | High Card | If no one has any of the above hands, |
| the player with the highest card wins |
Poker Hands Value
___________________________________________________________________________
Counting Poker Hands
Straight Flush
Counting from A-K-Q-J-10, K-Q-J-10-9, Q-J-10-9-8, …, 6-5-4-3-2 to 5-4-3-2-A, there are 10 hands that are in sequence in a given suit. So there are 40 straight flush hands all together.
Four of a Kind
There is only one way to have a four of a kind for a given rank. The fifth card can be any one of the remaining 48 cards. Thus there are 48 possibilities of a four of a kind in one rank. Thus there are 13 x 48 = 624 many four of a kind in total.
Full House
Let's fix two ranks, say 2 and 8. How many ways can we have three of 2 and two of 8? We are choosing 3 cards out of the four 2's and choosing 2 cards out of the four 8's. That would be = 4 x 6 = 24. But the two ranks can be other ranks too. How many ways can we pick two ranks out of 13? That would be 13 x 12 = 156. So the total number of possibilities for Full House is
Note that the multiplication principle is at work here. When we pick two ranks, the number of ways is 13 x 12 = 156. Why did we not use = 78?
Flush
There are = 1,287 possible hands with all cards in the same suit. Recall that there are only 10 straight flush on a given suit. Thus of all the 5-card hands with all cards in a given suit, there are 1,287-10 = 1,277 hands that are not straight flush. Thus the total number of flush hands is 4 x 1277 = 5,108.
Straight
There are 10 five-consecutive sequences in 13 cards (as shown in the explanation for straight flush in this section). In each such sequence, there are 4 choices for each card (one for each suit). Thus the number of 5-card hands with 5 cards in sequence is . Then we need to subtract the number of straight flushes (40) from this number. Thus the number of straight is 10240 – 10 = 10,200.
Three of a Kind
There are 13 ranks (from A, K, …, to 2). We choose one of them to have 3 cards in that rank and two other ranks to have one card in each of those ranks. The following derivation reflects all the choosing in this process.
Two Pair and One Pair
These two are left as exercises.

The number of possible 5-card poker hands would then be the same as the number of 5-element subsets of 52 objects. The following is the total number of 5-card poker hands drawn from a standard deck of 52 cards.
The notation is called the binomial coefficient and is pronounced 'n choose r', which is identical to the number of -element subsets of a set with objects. Other notations for are , and . Many calculators have a function for . Of course the calculation can also be done by definition by first calculating factorials.
Poker Value Chart
Thus the probability of obtaining a specific hand (say, 2, 6, 10, K, A, all diamond) would be 1 in 2,598,960. If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of all diamond cards? It is
This is definitely a very rare event (less than 0.05% chance of happening). The numerator 1,287 is the number of hands consisting of all diamond cards, which is obtained by the following calculation.
The reasoning for the above calculation is that to draw a 5-card hand consisting of all diamond, we are drawing 5 cards from the 13 diamond cards and drawing zero cards from the other 39 cards. Since (there is only one way to draw nothing), is the number of hands with all diamonds.
If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of cards in one suit? The probability of getting all 5 cards in another suit (say heart) would also be 1287/2598960. So we have the following derivation.
Thus getting a hand with all cards in one suit is 4 times more likely than getting one with all diamond, but is still a rare event (with about a 0.2% chance of happening). Some of the higher ranked poker hands are in one suit but with additional strict requirements. They will be further discussed below.
Another example. What is the probability of obtaining a hand that has 3 diamonds and 2 hearts? The answer is 22308/2598960 = 0.008583433. The number of '3 diamond, 2 heart' hands is calculated as follows:
One theme that emerges is that the multiplication principle is behind the numerator of a poker hand probability. For example, we can think of the process to get a 5-card hand with 3 diamonds and 2 hearts in three steps. The first is to draw 3 cards from the 13 diamond cards, the second is to draw 2 cards from the 13 heart cards, and the third is to draw zero from the remaining 26 cards. The third step can be omitted since the number of ways of choosing zero is 1. In any case, the number of possible ways to carry out that 2-step (or 3-step) process is to multiply all the possibilities together.
___________________________________________________________________________
The Poker Hands
Here's a ranking chart of the Poker hands.
The chart lists the rankings with an example for each ranking. The examples are a good reminder of the definitions. The highest ranking of them all is the royal flush, which consists of 5 consecutive cards in one suit with the highest card being Ace. There is only one such hand in each suit. Thus the chance for getting a royal flush is 4 in 2,598,960.
Royal flush is a specific example of a straight flush, which consists of 5 consecutive cards in one suit. There are 10 such hands in one suit. So there are 40 hands for straight flush in total. A flush is a hand with 5 cards in the same suit but not in consecutive order (or not in sequence). Thus the requirement for flush is considerably more relaxed than a straight flush. A straight is like a straight flush in that the 5 cards are in sequence but the 5 cards in a straight are not of the same suit. For a more in depth discussion on Poker hands, see the Wikipedia entry on Poker hands.
The counting for some of these hands is done in the next section. The definition of the hands can be inferred from the above chart. For the sake of completeness, the following table lists out the definition.
Definitions of Poker Hands
| Poker Hand | Definition | |
|---|---|---|
| 1 | Royal Flush | A, K, Q, J, 10, all in the same suit |
| 2 | Straight Flush | Five consecutive cards, |
| all in the same suit | ||
| 3 | Four of a Kind | Four cards of the same rank, |
| one card of another rank | ||
| 4 | Full House | Three of a kind with a pair |
| 5 | Flush | Five cards of the same suit, |
| not in consecutive order | ||
| 6 | Straight | Five consecutive cards, |
| not of the same suit | ||
| 7 | Three of a Kind | Three cards of the same rank, |
| 2 cards of two other ranks | ||
| 8 | Two Pair | Two cards of the same rank, |
| two cards of another rank, | ||
| one card of a third rank | ||
| 9 | One Pair | Three cards of the same rank, |
| 3 cards of three other ranks | ||
| 10 | High Card | If no one has any of the above hands, |
| the player with the highest card wins |
Poker Hands Value
___________________________________________________________________________
Counting Poker Hands
Straight Flush
Counting from A-K-Q-J-10, K-Q-J-10-9, Q-J-10-9-8, …, 6-5-4-3-2 to 5-4-3-2-A, there are 10 hands that are in sequence in a given suit. So there are 40 straight flush hands all together.
Four of a Kind
There is only one way to have a four of a kind for a given rank. The fifth card can be any one of the remaining 48 cards. Thus there are 48 possibilities of a four of a kind in one rank. Thus there are 13 x 48 = 624 many four of a kind in total.
Full House
Let's fix two ranks, say 2 and 8. How many ways can we have three of 2 and two of 8? We are choosing 3 cards out of the four 2's and choosing 2 cards out of the four 8's. That would be = 4 x 6 = 24. But the two ranks can be other ranks too. How many ways can we pick two ranks out of 13? That would be 13 x 12 = 156. So the total number of possibilities for Full House is
Note that the multiplication principle is at work here. When we pick two ranks, the number of ways is 13 x 12 = 156. Why did we not use = 78?
Flush
There are = 1,287 possible hands with all cards in the same suit. Recall that there are only 10 straight flush on a given suit. Thus of all the 5-card hands with all cards in a given suit, there are 1,287-10 = 1,277 hands that are not straight flush. Thus the total number of flush hands is 4 x 1277 = 5,108.
Straight
There are 10 five-consecutive sequences in 13 cards (as shown in the explanation for straight flush in this section). In each such sequence, there are 4 choices for each card (one for each suit). Thus the number of 5-card hands with 5 cards in sequence is . Then we need to subtract the number of straight flushes (40) from this number. Thus the number of straight is 10240 – 10 = 10,200.
Three of a Kind
There are 13 ranks (from A, K, …, to 2). We choose one of them to have 3 cards in that rank and two other ranks to have one card in each of those ranks. The following derivation reflects all the choosing in this process.
Two Pair and One Pair
These two are left as exercises.
Poker Starting Hands Expected Value
High Card
The count is the complement that makes up 2,598,960.
The following table gives the counts of all the poker hands. The probability is the fraction of the 2,598,960 hands that meet the requirement of the type of hands in question. Note that royal flush is not listed. This is because it is included in the count for straight flush. Royal flush is omitted so that he counts add up to 2,598,960.
Probabilities of Poker Hands
Poker Hands In Order Of Value
| Poker Hand | Count | Probability | |
|---|---|---|---|
| 2 | Straight Flush | 40 | 0.0000154 |
| 3 | Four of a Kind | 624 | 0.0002401 |
| 4 | Full House | 3,744 | 0.0014406 |
| 5 | Flush | 5,108 | 0.0019654 |
| 6 | Straight | 10,200 | 0.0039246 |
| 7 | Three of a Kind | 54,912 | 0.0211285 |
| 8 | Two Pair | 123,552 | 0.0475390 |
| 9 | One Pair | 1,098,240 | 0.4225690 |
| 10 | High Card | 1,302,540 | 0.5011774 |
| Total | 2,598,960 | 1.0000000 |
___________________________________________________________________________
2017 – Dan Ma

